Zapis realnih števil s plavajočo vejico

Besedilo vaje: Napišite program, ki s pomočjo Taylorjeve vrste izračuna sinus kota. Za zapis realnega števila x uporabite dve celi 16-bitni predznačeni števili, mantiso m in eksponent e, tako da velja x = m * 2^e. Program naj upošteva vse člene Taylorjeve vrste, katerih doprinos je z natančnostjo podanega zapisa realnega števila v končnem rezultatu še zaznaven.

Razlaga: Program napišete v razvojnem okolju, ki teče na osebnem računalniku. Pripravljen delovni prostor (angl. workspace) z vsemi pripadajočimi datotekami najdete tukaj. V njem se poleg nastavitev projekta nahajajo tudi datoteke s spremljajočo izvorno kodo. Po končanem zagonu pristanemo v funkciji start_up(), ki se nahaja v datoteki startup.c. Tu boste mikrokrmilnik inicializirali, kar naredite s klicem funkcije init(). Za njeno uporabo morate vključiti datoteko init.h. Lastno kodo te vaje boste dodali v funkciji main(), ki se nahaja v datoteki main.c.

Realna števila je možno zapisati s fiksno ali plavajočo vejico. Zapis s fiksno vejico je enostaven, vendar nenatančen in ima relativno majhen obseg. Zato se le redko uporablja. Pri zapisu s plavajočo vejico je realno število vedno podano z dvema celima številoma, mantiso in eksponentom. Kadar v programskem jeziku C uporabimo tip float ali double, se mantisa in eksponent zapišeta po standardu IEEE 754. Za zapis tipa float je potrebnih 32 bitov, natančnejši tip double pa je dolg 64 bitov. Kratek izvleček standarda IEEE 754 najdete tukaj. Zaradi kompaktnosti zapisa in obravnave posebnih vrednosti postane zbirniška koda z uporabo realnih števil dokaj zapletena. Zato ob mikroprocesorjih večkrat srečamo še koprocesor, ki je namenjen prav izvajanju operacij med števili zapisanimi s plavajočo vejico.

V naši vaji ne bomo uporabljali tipov float in double, pač pa le celoštevilske tipe. Zapis realnih števil je v primerjavi s standardom IEEE 754 močno poenostavljen. Zato bo kodiranje aritmetičnih operacij med našimi realnimi števili primerno preprostejše. Za primer si poglejmo zapis števila pi.

 pi = 3.14159... = 11.0010010000111...₂ = 0b0110010010000111 * 2^-13 = 0x6487 * 2^0xfff3

Število pi bi torej zapisali z dvema 16-bitnima številoma pi_m in pi_e.

 short int pi_m = 0x6487, pi_e = 0xfff3;

S pomočjo Taylorjeve vrste moramo izračunati sinus kota podanega v radianih. Velja:

 sin(x) = x - x³ / 3! + x⁵ / 5! - x⁷ / 7! + ...

Da bomo to lahko naredili, potrebujemo vse štiri aritmetične operacije: seštevanje, odštevanje, množenje in deljenje. V zapisu s plavajočo vejico je najenostavneje narediti množenje. Mantisi zmnožimo, eksponenta pa seštejemo. Velja:

 x1 = m1 * 2^e1      x2 = m2 * 2^e2      x1 * x2 = m1 * m2 * 2^{(e1 + e2)}

Da se izognemo nevšečnostim zaradi končnega obsega, obe mantisi in oba eksponenta pred uporabo razširimo v 32-bitna števila tipa int. Mantisa in eksponent produkta, m1*m2 in e1+e2, sta tako 32-bitni predznačeni števili. Ker realna števila zapisujemo s pari 16-bitnih predznačenih števil, ju moramo skrčiti nazaj v 16-bitni zapis. To naredimo s klicem funkcije adjust(), ki je že podana v datoteki main.c. Funkcija prejme kazalca na mantiso in eksponent in ju predela v 16-bitna ekvivalenta. Sledi primer kode, ki razširjeni zapis (m32, e32) pretvori v 16-bitnega (m16, e16).

  short int m16, e16;
  int m32, e32;
   ...
  adjust(&m32, &e32);
  m16 = (short int)m32;
  e16 = (short int)e32;

Če je realna vrednost v razširjenem zapisu prevelika (premajhna) in je s 16-bitnim parom ne moremo zapisati, funkcija adjust() vrne največje (najmanjše) možno število. Začasno pretvorbo v 32-bitni zapis in nazaj uporabimo tudi pri ostalih aritmetičnih operacijah.

Seštevanje zahteva nekaj več truda. Eksponenta moramo najprej izenačiti, nakar mantisi seštejemo. Manjši eksponent povečujemo toliko časa, dokler ni enak večjemu. Algoritem podaja spodnja slika.

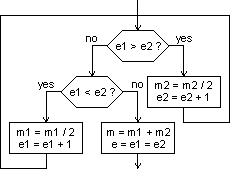
Podobno velja za odštevanje.

Deljenje dveh realnih števil zapisanih s plavajočo vejico je zahtevnejše. Velja:

 x1 = m1 * 2^e1      x2 = m2 * 2^e2      x1 / x2 = m1 / m2 * 2^{(e1 - e2)}

Kvocient m1/m2 je sam po sebi realno število. Zato ga množimo z dva (pomik v levo) toliko časa, dokler v okviru 16-bitnega zapisa ne dobimo celega števila. Ob vsakem množenju eksponentu kvocienta e1-e2 seveda odštejemo ena. Algoritem podaja spodnja slika. Znak / označuje celoštevilsko deljenje, medtem ko znak % pomeni deljenje po modulu.

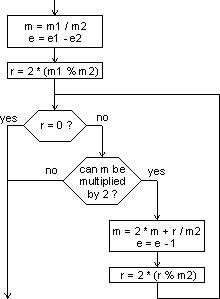
Ko imamo realizirane vse štiri aritmetične operacije, je izvedba naše naloge preprosta. V neskončni zanki izračunavamo člene Taylorjeve vrste in jih prištevamo h končnemu rezultatu. To počnemo toliko časa, dokler ne pridemo do člena, ki na rezultat zaradi končne točnosti zapisa realnih števil nima vpliva. Algoritem podaja spodnja slika.

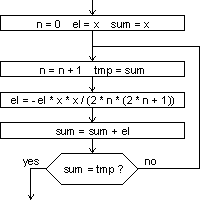
V algoritmu je uporabljena enačba

 a_n = - a_{n - 1} * x² / (2 * n * (2 * n + 1)) ,

ki podaja naslednji člen v Taylorjevi vrsti.

V razmislek. V vaji smo realizirali računanje z realnimi števili brez uporabe tipov float ali double. Z uporabo enega ali drugega tipa lahko enak program, ki izračuna vrednost funkcije sinus s seštevanjem členov Taylorjeve vrste, zelo hitro realizirate. Izvorna koda v programskem jeziku C bo mnogo krajša in kompaktnejša, vendar bo prevedena zbirniška koda zaradi zapisa realnih števil po standardu IEEE 754 daljša. Za izvršitev bo zato potrebno tudi več procesorskega časa.