Initial conditions in the circuit can be set in two ways. First we can put an .ic statement, which defines node voltages at time 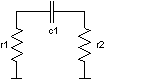t = 0. Or second we can set an ic parameter of a device instance (for example capacitor or inductor), which defines initial instance voltage or current. Let us examine a simple circuit with one capacitor and two resistances.

r1 1 0 1
r2 2 0 1
c1 1 2 1

If we define an initial state with only one nodal voltage by .ic statement

.ic v(1)=1V

then the initial voltage v(2) is left undefined and it equals to zero by default. Therefore the initial voltage on capacitor c1 is 1V. The same effect can be obtained by defining

.ic v(1)=2V v(2)=1V

Again the initial voltage on capacitor c1 is 1V. Both examples are equivalent to defining initial capacitor voltage by

c1 1 2 1 ic=1V

If there is a nonsense like

c1 1 2 1 ic=1V
.ic v(1)=10V v(2)=1V

then ic parameter at element instance definition is considered. 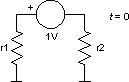So the initial capacitor voltage v(1,2) is 1V in all four cases above. At the time t = t₀ = 0 the circuit, where capacitors are replaced by voltage sources and inductors by current sources, has to be solved to obtain initial node voltages, in our case v(1) and v(2). By solving this circuit we get v(1) = 0.5V and v(2) = -0.5V. But that is not the case in SPICE, which does not perform any analysis, but simply copies the .ic values as solutions for t = t₀ = 0. So

• in the first case we get v(1) = 1V and v(2) = 0,
• in the second case we get v(1) = 2V and v(2) = 1V,
• in the third case we get v(1) = 0 and v(2) = 0 and
• in the fourth case we get v(1) = 10V and v(2) = 1V.

All four results are wrong. The only way to get a correct result for t = t₀ = 0 is putting the statement

.ic v(1)=0.5V v(2)=-0.5V

In the first time point 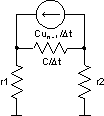t = t₁ an appropriate associated resistive circuit is solved (see figure below). All capacitors and inductors are replaced by current source in parallel with resistance. Backward Euler algorithm (first order algorithm) is always used in the first time point, regardless to chosen trapezoidal or Gear integrating algorithm and the integration order (given by method and maxord simulator options).

t = t₁, n = 1
u_{n - 1} = u_{t = 0} ... initial capacitor voltage, in our case 1V

Dt = t₁ - t₀ = t₁

Solving this circuit gives a correct results for t = t₁ and all following t = t₂, t₃ ... time points. The integration order is also increased in further simulation. The only problem that remains are wrong results for t = 0. This error can be eliminated by icstep simulator option. It uses the fact that the circuit in the second figure gives the same results as the circuit in the third figure for Dt limiting towards 0. So before the circuit is analysed at t = t₁, it is analysed at t = t₁ / icstep. The results of this "initial" analysis are proclaimed as "initial" solution of the circuit for t = 0. If icstep is large, than this solution is near the exact solution of the circuit shown in the second figure. If parameter icstep is less than 1, it is ignored. The default value is 0.

So if the user wants to have a correct initial value in the resulting plot (solution vectors), than he has to include an appropriate .ic statement or he has to set the icstep simulator parameter. In the first case he has to know the initial node voltages, which is not usual. In the second case the simulator will work transparently and the initial node voltages will be at least very near to the right ones. In our example circuit we would reach this goal by issuing following line

.options icstep=1e9

icstep simulator parameter can also be changed through set command like all other parameters.