5.5. pyopus.problems.mwbm — More-Wild set of test functions for DFO, data profile generation¶

Derivative-free optimization test functions by More and Wild. (PyOPUS subsystem name: MWBM)
All 22 basic test functions [mw] in this module are maps from  to
to
 . All functions are unconstrained. Every function comes from the
CUTEr test set and is specified by a tuple (mgh_name, n, m, s), where n is the
dimension, m is the number of component functions, and s specified the initial
point scaling, i.e.
. All functions are unconstrained. Every function comes from the
CUTEr test set and is specified by a tuple (mgh_name, n, m, s), where n is the
dimension, m is the number of component functions, and s specified the initial
point scaling, i.e.
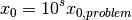
Every problem can be smooth, piecewise-smooth, deterministically noisy or stochastically noisy.
The CUTEr problems used by this suite are implemented in the _mwbm module. This module does not depend on CUTEr.
This module is independent of PyOPUS, meaning that it can be taken as is and used as a module in some other package. It depends only on the cpi and the _mwbm modules.
Beside test functions this module also includes support for data profile generation from function value history.
| [mw] | More, J.J., Wild S.M., Benchmarking Derivative-Free Optimization Algorithms. SIAM Journal on Optimization, vol. 20, pp.172-191, 2009. |
-
class
pyopus.problems.mwbm.MWBM(num, problemType=0, epsilon=0.001)¶ Test functions from the More-Wild suite.
num is the problem number (0-52).
problemType is the type of the problem (0=smooth, 1=piecewise smooth, 2=deterministically noisy, 3=stochastically noisy).
epsilon is the noise level for problemType 2 and 3.
The number of the underlying function (0-21) is stored in
probNdx. The dimension, the number of component functions, and the initial point scaling are stored in then,m, andsmembers.The full name of the problem is in the
namemember. It is of the form name_m_s.The initial point can be obtained from the
initialmember. The function value is returned by thef()method.The gradient and the best known minimum of the function are not available.
-
cpi()¶ Returns the common problem interface.
xmin, fmin, and g are not available.
The info member of the returned dictionary is itself a dictionary with the following members:
m- m parameter of the MWBM problems- s parameter of the MWBM problem
See the
CPIclass for more information.
-
descriptors= [[1, 9, 45, 0], [1, 9, 45, 1], [2, 7, 35, 0], [2, 7, 35, 1], [3, 7, 35, 0], [3, 7, 35, 1], [4, 2, 2, 0], [4, 2, 2, 1], [5, 3, 3, 0], [5, 3, 3, 1], [6, 4, 4, 0], [6, 4, 4, 1], [7, 2, 2, 0], [7, 2, 2, 1], [8, 3, 15, 0], [8, 3, 15, 1], [9, 4, 11, 0], [10, 3, 16, 0], [11, 6, 31, 0], [11, 6, 31, 1], [11, 9, 31, 0], [11, 9, 31, 1], [11, 12, 31, 0], [11, 12, 31, 1], [12, 3, 10, 0], [13, 2, 10, 0], [14, 4, 20, 0], [14, 4, 20, 1], [15, 6, 6, 0], [15, 7, 7, 0], [15, 8, 8, 0], [15, 9, 9, 0], [15, 10, 10, 0], [15, 11, 11, 0], [16, 10, 10, 0], [17, 5, 33, 0], [18, 11, 65, 0], [18, 11, 65, 1], [19, 8, 8, 0], [19, 10, 12, 0], [19, 11, 14, 0], [19, 12, 16, 0], [20, 5, 5, 0], [20, 6, 6, 0], [20, 8, 8, 0], [21, 5, 5, 0], [21, 5, 5, 1], [21, 8, 8, 0], [21, 10, 10, 0], [21, 12, 12, 0], [21, 12, 12, 1], [22, 8, 8, 0], [22, 8, 8, 1]]¶ Problem descriptors (problem number, n, m, s)
-
namelist= ['LinearFullRank', 'LinearRank1', 'LinearRank1ZCR', 'Rosenbrock', 'HelicalValley', 'PowellSingular', 'FreudensteinAndRoth', 'Bard', 'KowalikAndOsborne', 'Meyer', 'Watson', 'Box3D', 'JennrichAndSampson', 'BrownAndDennis', 'Chebyquad', 'BrownAlmostLinear', 'Osborne1', 'Osborne2', 'Bdqrtic', 'Cube', 'Mancino', 'Heart8']¶ List of problem names
-
Example file mwbm.py in folder demo/problems/
# Demo of the More-Wild problems
from pyopus.problems.mwbm import MWBM
if __name__ == '__main__':
# Every problem is described by an entry in the list of descriptors.
# We use this list to get a problem count.
for ii in range(len(MWBM.descriptors)):
# Create the default (smooth) problem
problem=MWBM(ii, problemType=0)
# Set problemType to
# 1 for piecewise-smooth problems
# 2 for deterministically noisy problems
# 3 for stochastically noisy problems
cpi=problem.cpi()
print(
"%2d: %25s n=%2d m=%2d s=%2d f0=%e" %
(
ii,
cpi['name'],
cpi['n'],
cpi['info']['m'],
cpi['info']['s'],
cpi['f'](cpi['x0'])
)
)